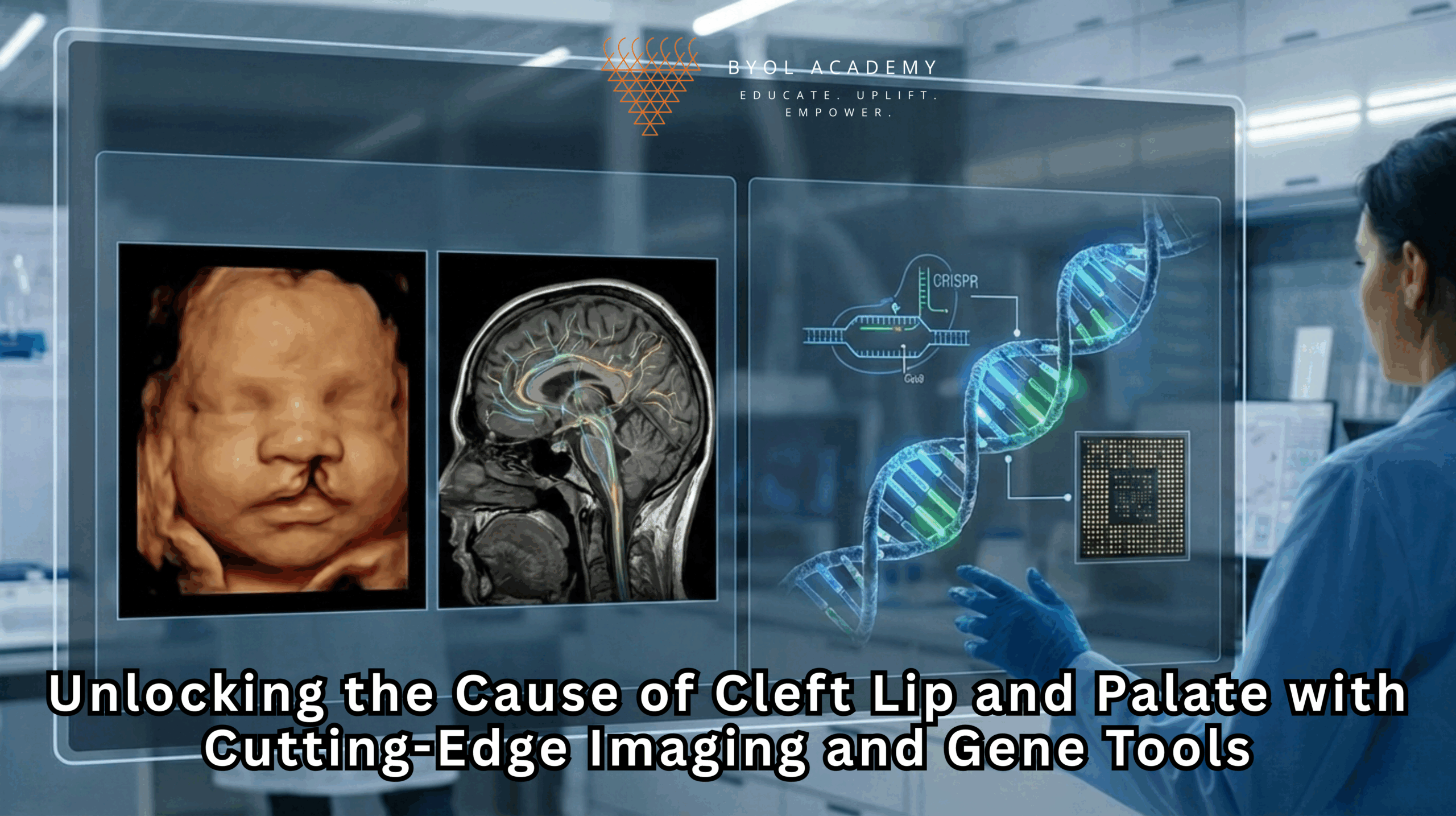
Every face tells its own story. Genetics shapes much of that story, but when key developmental instructions go awry, babies […]
In the realm of logical reasoning, one topic recurs frequently in exams, puzzles and everyday thinking that is blood relation. At first glance, “blood relation” may sound like a purely biological or genealogical concept who is related to whom by birth. But in reasoning problems, it is elevated into a structured logic framework, where you must decode relationships given indirect clues. Whether you are solving competitive exam questions, verifying family trees, or simply trying to understand who is whose aunt/uncles/nephew in a roundabout scenario blood relation reasoning helps. In this article, we explore what blood relation means, the types of blood-relation problems, formulas and techniques to solve them, real-life applications, and why mastering this topic is valuable.
So, what exactly is blood relation? In general usage, a “blood relation” refers to a connection between two or more individuals that arises through birth. for example, parents, child, siblings, grandparents, etc.
In the context of reasoning (verbal/aptitude reasoning), the term expands slightly, it includes both birth based relations (like father, mother, brother, sister, son, daughter) and relations by marriage (like father in law, mother in law, son in law, daughter in law) depending on how questions are framed.
In reasoning tests, blood relation problems describe the relationships between various family members using statements or codes, and the solver’s task is to deduce how two specified individuals are related.
Thus, blood relation reasoning is the exercise of using given relational information to map out or deduce family links logically.
In reasoning contexts, blood relation questions come in various formats. Understanding these types is helpful before you attempt to solve them. Commonly, the following categories are recognized:
Because blood relation reasoning is more about logic than numeric formulas, there’s no mathematical formula per se. However, over time, the reasoning community has developed a kind of “mental formula / approach” a systematic method to decode relationships quickly. Below is a step by step “formulaic” approach, followed by examples.
Question: A is the brother of B. B is the mother of C. How is A related to C?
Solution (using the “formula” approach):
1. B is mother of C → so B is one generation above C.
2. A is the brother of B → A is sibling to C’s mother → So A is C’s maternal uncle.
Answer: A is the uncle of C.
Solution:
1. John → father of Mary.
2. Mary → mother of Sam.
So John is the grandfather of Sam.
Answer: John is Sam’s grandfather.
Question : P says, “Q is the son of the only daughter of my father.” What is Q’s relation to P?
Solution (step by step):
1. “My father” → father of P.
2. “The only daughter of my father” → that is P’s sister if P is not female; but careful: that phrase could also be P herself if P is female. Usually in these problems we assume P is male unless otherwise stated, but safer: parse both possibilities. However most common intended reading, the only daughter of P’s father is P’s sister (if P is male) or P (if P is female). Competitive problems usually imply the speaker is male unless stated. To avoid ambiguity these problems often implicitly mean P is male. We’ll assume P is male.
3. So the only daughter of P’s father = P’s sister.
4. Q is the son of that sister → Q is P’s nephew.
Answer: Q is P’s nephew.
(If P were female and the only daughter is P herself, then Q would be P’s son, but that reading is less common unless specified.)
Example 3 : Tricky (nested relation)
Solution:
1. B’s mother’s only child → that child could be B (if B is the only child) or B’s sibling, but phrase “only child” means there is exactly one child, so it must be B.
2. So B’s mother’s only child = B.
3. A is the son of B → A is B’s son.
Answer: A is B’s son.
Example 4 : Multi-step with cousins
Solution:
1. M and N → siblings.
2. P is M’s son; Q is N’s daughter.
3. Children of two siblings are first cousins.
Answer: P and Q are first cousins.
Suppose a code language defines:
Solution:
1. P + Q means P is mother of Q → Q is child of P.
2. Q – R means Q is brother of R → R is sibling of Q (thus also a child of P).
3. R ÷ S means R is father of S → S is child (grandchild of P).
4. S × T means S is wife of T → T is husband of S.
So, person T is the husband of S, S is child of R, R is child of P. Thus, T is son-in-law (or rather “daughter’s husband / son-in-law”) of P.
This is a typical coded blood relation problem.
Question: (Hypothetical) “Riya is the daughter of Mani. Abhishek is the father of Siya. Riya is married to Danish. Riya and Siya are siblings. Raghav is the brother of Danish. Mani has only one daughter. Sneha is the daughter of Riya. Raghav is the father of Akshay. What is the relation between Raghav and Akshay?”
Solution Outline:
Riya is daughter of Mani. Mani has only one daughter → Riya is Mani’s only child.
1. Riya married Danish. So Danish is Riya’s husband.
2. Riya has a daughter Sneha. (Sneha is child of Riya & Danish.)
3. Raghav is brother of Danish → Raghav is Riya’s brother in law.
4. Raghav is father of Akshay → Akshay is child of Raghav.
So what is Raghav’s relation to Akshay? He is father. But what is Akshay to Riya’s family? He is nephew (child of husband’s brother) of Riya.
This is how a multi statement family tree puzzle can be solved by building a mental (or drawn) family tree and walking generation by generation. This type of question is common in reasoning sections.
Solution:
1. “My grandfather” → X’s grandfather.
2. “The only daughter of my grandfather” → the granddaughter of the grandfather who is the only daughter. That person could be X’s mother or X’s aunt or X herself, depending on gender and generations. But because it’s “only daughter of my grandfather,” possibilities:
If the grandfather’s only daughter is X’s mother (meaning X’s grandmother + grandfather had one daughter who is X’s mother), then that only daughter = X’s mother.
If the only daughter = X herself (if X is female and the only daughter), then ambiguous. Competitive problems usually intend a single interpretation: that the “only daughter of my grandfather” is X’s mother.
3. So Y is the son of X’s mother → Y is X’s brother.
Answer: Y is X’s brother.
(If X were female and herself the only daughter, Y would be X’s son, but this reading is rarely intended.)
Q: Pointing to a photograph, a man says, “This man’s son is the only son of my father.” The man in the photograph is the son of whom?
A) His brother
B) His father
C) His son
D) His grandson
Solution:
→Interpret the sentence carefully: “This man’s son is the only son of my father.”
→“The only son of my father” = the speaker himself if the speaker is the only son (most natural reading), i.e., the only male child of his father is the speaker. So the only son of my father = me (the speaker).
→So “This man’s son = me.” That means the speaker is the son of the man in the photograph.
Therefore the man in the photograph is the speaker’s father.
Answer: B) His father.
Beyond competitive exams and puzzles, blood-relation reasoning has several real-life applications:
Understanding and mastering blood relation reasoning is important for several reasons:
Blood relation reasoning might at first appear like a niche topic only useful for competitive exams. But in reality, it is much more than that. It is a systematic way of thinking about human relationships, genealogies, and family structures. Whether you are verifying your family tree, deciding on inheritance, tracking genetic medical history, or simply solving a tricky reasoning question, a clear and logical understanding of blood relations proves immensely useful.
If you practise it regularly, using diagrams or coded relations, you not only become quick at solving puzzles, but also sharpen your logical reasoning skills a tool that remains valuable well beyond exams.
In summary, “blood relation” in reasoning is not just about knowing who is whose father or mother, brother or sister. It is a logical framework for analyzing familial connections given indirect, coded or multi step information. There are several types of blood relation problems direct, indirect, coded, pointing, mixed puzzles each requiring slightly different strategies. By using a methodical approach (defining persons, breaking down statements, avoiding assumptions, drawing family trees), one can decode relationships accurately.
Beyond exams, these skills have real life significance: from building family trees, dealing with inheritance or medical distributions, to organizing records blood-relation reasoning helps us model our social world more clearly. If cultivated carefully, this reasoning ability becomes part of your mental toolkit, enabling sharper analysis, deeper understanding of social and familial ties, and better decision making.
Every face tells its own story. Genetics shapes much of that story, but when key developmental instructions go awry, babies […]
A major advancement in vision science has revealed a previously unrecognized genetic risk for severe age-related macular degeneration (AMD), the […]
Introduction Reasoning ability forms the foundation of logical thinking, decision-making, and problem-solving. Whether a student prepares for competitive exams or […]